Физическая динамическая нагрузка

Динамическая работа

ФИЗИОЛОГИЧЕСКАЯ ХАРАКТЕРИСТИКА МЫШЕЧНОЙ РАБОТЫ

Мышечная работа (М.р.) — перемещение и поддержание полог, жений тела и его частей благодаря работе мышц, обеспечиваемой координацией всех физиологических процессов в организме. Раз­личные группы мышц находятся в сложном взаимодействии между собой и с различными механическими силами — тяжести, инерции и пр. Различают динамическую работу при движениях в суставах и статические усилия для поддержания неподвижного положе­ния. Важной характеристикой динамической работы являются ве­личины затрат энергии на ее выполнение.

Вид мышечной работы, характеризуемый периодическими со­кращениями и расслаблениями скелетных мышц с целью переме­щения тела или отдельных его частей, а также выполнения опреде­ленных рабочих действий. Физиологические реакции при динамической работе (возрастание ЧСС, АД, ударного и минутного объема крови, изменения регионарного и общего сосудистого сопротивления и др.) зависят от силы и частоты сокращений, раз­меров работающих мышц, степени тренированности человека, по­ложения тела, в котором выполняется работа, условий окружаю­щей среды.

М.р. принято называть общей, если в ней участвует более двух третей всей скелетной мускулатуры, регионарной — от одной до двух третей и локальной — менее трети всей массы скелетной мус­кулатуры.

Количественные показатели М.р. характеризуют двигательную активность.

Двигательная активность (Д.а.) — общее количество мышеч­ных движений, регулярно выполняемых данным человеком. Уро­вень Д.а. связан с особенностями труда, быта и отдыха.

Отклонения от оптимального диапазона действуют неблагопри­ятно. Чрезмерная мышечная работа приводит к переутомлению и перенапряжению, недостаточная Д.а. (гиподинамия) — к фи­зической детренированности. Резко выраженные крайности сопро­вождаются стрессом.

Уровень двигательной активности (Д.а.) оценивают по сумме затрат энергии и иногда по сумме сокращений сердца сверх уровня покоя, в среднем — за определенное время. Часто используют под­счет какого-либо вида мышечных движений, составляющих суще­ственную часть общей Д.а. за час, сутки или иной период (напри­мер, количество пройденных шагов, в спорте — сумма пробегаемых или проплываемых отрезков дистанции) и т. п.

Статическая работа

Вид мышечной работы, характеризуемый непрерывным сокра­щением скелетных мышц с целью удержания тела или отдельных частей, а также выполнения определенных трудовых действий. При статической работе, в отличие от динамической, имеют место весь­ма незначительные увеличения потребления кислорода и минутно­го объема крови. При этом существенно возрастают ЧСС, АД, ЧД и общее периферическое сопротивление сосудов. Физиологические реакции сердечно-сосудистой системы при статической работе за­висят от силы и продолжительности сокращения мышц. В случае работы до сильного утомления при равных величинах относитель­ных усилий эти реакции мало зависят от размеров работающих мышц.

dinamitri494

Статическая работа.

Она характеризуется тем, что напряжение мышц развивается без изменения длины последних и без активного перемещения конечностей и всего тела.
При статическом усилии с точки зрения физики внешняя механическая работа отсутствует, однако в физиологическом смысле она характеризуется теми активными процессами, которые протекают в нервно — мышечном аппарате и центральной нервной системе, обеспечивая поддержание напряженного состояния мышц.

Статическая работа характеризуется быстрым утомлением, поскольку напряжение мышц длится непрерывно, без пауз, не допуская отдыха. При статической работе кровообращение в мышцах затруднено, что приводит к застою крови и накоплению неокисленных продуктов в организме в целом. При статической работе наблюдается незначительное увеличение потребления кислорода, но после её прекращения потребление кислорода резко возрастает и усиливается кровоток (феномен Лингарда, рис.).

В ряде случаев и другие физиологические показатели (частота пульса, дыхание и др.) непосредственно
после статической работы увеличиваются. При длительном поддержании статического напряжения утомление мышц, сочетаясь с недостаточным кровоснабжением, может привести к развитию заболеваний мышечной и нервной систем.

Динамическая работа.

Это процесс сокращения мышц, приводящий к перемещению груза, а также тела человека или его частей в пространстве. Динамическая работа всегда в какой-то степени сочетается со статической.
Динамическая работа бывает: общая, региональная и локальная. Общая мышечная работа выполняется более чем двумя третями массы скелетной мускулатуры. Это работы, где полностью или в значительной степени отсутствует механизация. Такие виды работ характеризуются высокими энергетическими затратами, низкими интеллектуальными и эмоциональными напряжениями.
Динамика потребления О2 в процессе динамической (физической) работы приведена
на рис.
t, мин

В начале работы наблюдается постепенное возрастание потребления О2. Оно происходит до тех пор,
пока не будет исчерпана ёмкость кислородоснабжающих органов и не достигнут предельный уровень потребления О2 данным индивидуумом, так называемый кислородный потолок.

Если затраты энергии (потребление кислорода как показатель энергозатрат) не выше кислородного потолка, наступает равновесие между скоростью образования и удаления продуктов распада.
При более высоких энергозатратах образуется кислородный дефицит и в организме идут накопление недоокислившихся продуктов, загрязнение организма, приводящее к появлению усталости.
Доокисление в организме продуктов жизнедеятельности происходит после окончания работы — идёт погашение кислородного долга.

Кислородный долг рассматриваетсякак часть кислородного запроса. Кислородный запрос — это количество кислорода израсходованного на протяжении работы и ближайшего восстановительного периода.

Динамическая работа менее утомительна, благодаря чередованию процессов сокращения и расслабления мышц, имеются паузы, во время которых нервные центры не посылают импульсов к мышцам и отдыхают.

Региональная мышечная работа выполняется мускулатурой плечевого пояса и рук. В ней участвуют от 1/3 до 2/3 массы
скелетной мускулатуры. Локальная мышечная работа выполняется менее 1/3 скелетных мышц. В условиях современного производства выполняются в основном региональная или локальная мышечная работа, требующие точности, координированности и быстрых движений.

Нагрузки (виды нагрузок, единицы измерения нагрузок).

Стр 1 из 4

Нагрузки (виды нагрузок, единицы измерения нагрузок).

Нагрузки – это внешние силы, действующие на конструкцию.

Сила – это мера механического воздействия одного тела на другое.

Единица измерения – ньютон (Н).

1Н = 1кг •м/с2

Также приблизительно можно принять:

1кг = 10Н

1кН =1000Н =100кг

1тонна =1000кг =10000Н =10кН

Нагрузки подразделяются:

а) По длительности воздействия – постоянные, временные, переменные.

Б) По характеру приложения – распределённые и сосредоточенные.

В) По характеру воздействия – статические и динамические.

Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.

Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.

Расчетные схемы.

При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.

Внутренние силовые факторы, метод сечений.

При действии на тело внешних сил внутри тела возникают силы сопротивления, которые называются внутренними силовыми факторами.

При различных видах деформаций возникают определённые внутренние силовые факторы. Всего при различных видах деформаций возникает шесть внутренних силовых факторов, которые характеризуют все виды деформаций, существующие в природе.

1. N – продольная сила, возникает при деформации растяжение и сжатие.

2. QХ

3. QУ

Это поперечные силы, возникают при деформации сдвиг.

4. МХ

5. МУ

Это изгибающие моменты, возникают при деформации изгиб.

6. МZ =Т – крутящий момент, возникает при деформации кручение.

Чтобы вычислить внутренние силовые факторы, применяется метод сечений, который заключается в том, что тело мысленно рассекается на две части, одна часть отбрасывается, а другая рассматривается и вместо отброшенной части прикладываются внутренние силовые факторы. Значения внутренних силовых факторов вычисляются из уравнений равновесия.

Напряжение.

Нормальное напряжение.

Касательное напряжение.

Напряжение – это мера интенсивности действия внутренних сил.

При действии на конструкцию внешней нагрузки в материале конструкции возникает механическое напряжение, которое характеризует интенсивность внутренних сил. Если нагрузку постепенно увеличивать, то значение напряжения тоже будет увеличиваться, и когда оно достигнет какого – то критического значения, произойдёт разрушение материала.

Полное напряжение р разложим на две оси, одна из них перпендикулярна к поперечному сечению конструкции, другая параллельна.

Получим следующее:

σ – нормальное напряжение, возникает при деформации растяжение или сжатие, всегда направлено перпендикулярно к поперечному сечению конструкции.

τ – касательное напряжение, возникает при деформации сдвиг, всегда направлено параллельно к поперечному сечению конструкции.

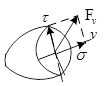Всегда нормальное и касательное напряжение взаимно перпендикулярны.

Рассмотрим нормальное напряжение. Оно вычисляется по следующей формуле:

σ =N/S

где S – площадь поперечного сечения конструкции

Единица измерения напряжения (Н/м2 ) =Па

Так как величина Па очень маленькая, то на практике применяют величину

(Н/мм2 ) =МПа

– допускаемое нормальное напряжение, каждый материал имеет своё значение.

Чтобы обеспечить прочность конструкции, значение напряжения не должно превышать допускаемого, иначе может произойти разрушение материала.

Приблизительные значения допускаемого нормального напряжения для некоторых материалов:

Сосна: = 8 МПа

Дуб: = 12…15 МПа

Алюминий: = 30…100 МПа

Медь: = 40…120 МПа

Ст 3: = 160 МПа

Сталь 45: = 240…360 МПа

Легированные высококачественные стали: = 400 МПа и выше

Вольфрам: = 500 МПа

Рассмотрим касательное напряжение. Оно вычисляется по следующей формуле:

τ =Q/S

– допускаемое касательное напряжение, каждый материал имеет своё значение.

Для большинства материалов = 0,6•

Деформации и перемещения.

Деформация – это изменение формы и объёма тела.

Деформация бывает упругой и пластичной. При упругой деформации тело полностью восстанавливает свою первоначальную форму и размеры после снятия нагрузки, а при пластичной нагрузке этого не происходит.

Деформация также бывает линейной и угловой.

Расчёт на прочность при растяжении и сжатии.

Условие прочности при растяжении и сжатии – нормальное напряжение не должно превышать допускаемого значения.

Основное уравнение прочности при растяжении и сжатии выглядит следующим образом:

σ max = N/S ≤

Расчёт на прочность при растяжении и сжатии можно также проводить через коэффициент запаса прочности

n – коэффициент запаса прочности

n = σт / σ

– минимально допустимый коэффициент запаса прочности

При статической нагрузке =1,5

Чтобы обеспечить прочность, должно соблюдаться условие:

n ≥

Температурные напряжения.

При нагреве или охлаждении металлического стержня его длина изменяется. Удлинение от действия температуры вычисляется по формуле

Δl =α•l• Δt

где α – коэффициент температурного расширения, величина табличная.

Например, для стали α = 1,25·10 – 5 1/град

Δt – изменение температуры

В связи с нагревом или охлаждением в металлических конструкциях могут возникнуть дополнительные температурные напряжения. Вычислив удлинение от действия температуры, из формулы (3) можно вычислить температурные напряжения.

Монтажные напряжения.

Часто встречаются случаи, когда стержневые элементы конструкций изготавливаются короче или длиннее проектной длины. При монтаже конструкции такие стержни приходится растягивать или укорачивать, что приводит к возникновению дополнительных монтажных напряжений. Эти напряжения можно вычислить из формулы (3).

16. Сдвиг (основные понятия и определения), расчёт на прочность при сдвиге.

Сдвиг – это такой вид деформации, при котором в поперечном сечении бруса возникает следующий внутренний силовой фактор – поперечная сила Q.

Деформация сдвиг ещё называется срез.

При сдвиге действует касательное напряжения τ, которое вычисляется по следующей формуле

τ = Q/S (7)

Деформация при сдвиге называется углом сдвига γ, вычисляется по следующей формуле

γ = Q/GS (8)

где G – модуль упругости ΙΙ рода, или модуль сдвига, характеризует жесткость бруса при сдвиге, величина табличная.

Для большинства материалов G = 0,4•E

Величина GS называется жёсткостью при сдвиге.

Подставим выражение (7) в выражение (8), получим

γ = τ /G (9)

или

τ = γ•G (10)

Выражения (9) и (10) являются законом Гука при сдвиге, который формулируется следующим образом: напряжение прямо пропорционально углу сдвига.

Единица измерения угла сдвига – радиан, можно перевести в градусы.

Условие прочности при сдвиге – касательное напряжение не должно превышать допускаемого значения.

Основное уравнение прочности при сдвиге выглядит следующим образом:

τ max = Q/S ≤

Примеры расчёта конструкций, работающих на сдвиг.

Рассмотрим заклёпочное соединение, на которое действуют сила F, направленная перпендикулярно осям заклёпок.

Условие прочности такого соединения имеет вид:

τ = Q/S ≤

В данном случае Q =F;

S – площадь поперечного сечения всех заклёпок;

S = S1• z

где S1 – площадь поперечного сечения одной заклёпки

S1 = (πd2)/4

z – число заклёпок

Рассмотрим сварное соединение внахлёстку, на которое действует сила F.

Условие прочности такого соединения имеет вид:

τ = Q/S ≤

В данном случае Q =F;

S – расчётная площадь сварного шва

S = 0,7•k•(2•L+2•b)

где k – катет сварного шва

Обычно k = 2…5мм

L – длина сварного шва по длине соединения

b – длина сварного шва по ширине соединения

Кинематические пары.

Примеры кинематических пар в зависимости от классов.

Кинематическая пара – соединение двух соприкасающихся звеньев, допускающее их относительное движение.

Элемент кинематическая пары – совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару

Кинематические пары различают и классифицируют по различным признакам.

1) По числу связей, налагаемых на относительное движение звеньев.

Всякое свободно движущееся в пространстве абсолютно твердое тело обладает шестью степенями свободы или шестью видами независимых возможных движений. Вхождение двух звеньев в кинематическую пару налагает на их относительное движение некоторые ограничения или условия связи; класс кинематической пары (номер класса совпадает с числом условий связи S) всегда находится в пределах от 1 до 5, число оставшихся подвижностей H дополняет число связей до шести, т.е. , поэтому пару пятого класса называют одноподвижной, четвертого – двухподвижной и т.д.

На рис. 3 представлены примеры кинематических пар 1 – 5 классов.

2) По характеру контакта звеньев различают пары низшие (требуемое относительное движение звеньев можно получить постоянным соприкасанием их элементов по поверхности) и высшие (требуемое относительное движение можно получить только соприкасанием их элементов по линиям и в точках). Например, трехподвижная пара по
рис. 3, в – низшая, а четырехподвижная по рис. 3, б – высшая.

3) По области относительного движения звеньев пары могут быть плоскими (траектории всех точек в относительном движении звеньев – плоские кривые, расположенные в параллельных плоскостях) и пространственными.

Плоская одноподвижная пара может быть либо вращательной (шарниром – рис. 3, д), либо поступательной (рис. 3, е); пространственная пара может быть, например, винтовой (одноподвижная), цилиндрической (двухподвижная), сферической (двух- и трехподвижная) и т.д.

Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.

а – пятиподвижная пара (1 класс)	б – четырехподвижная пара (2 класс)
в – трехподвижная пара (3 класс)	г – двухподвижная пара (4 класс)
д – одноподвижная вращательная пара (5 класс)	е – одноподвижная поступательная пара (5 класс)
Рис. 3

Кинематические цепи.

Систему звеньев, связанных между собой кинематическими парами, называют кинематической цепью.

Классификация кинематических цепей

1) По области движения звеньев цепи бывают плоские (траектории движения точек всех звеньев –– плоские кривые, лежащие в параллельных плоскостях) и пространственные.

2) По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем в две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.

3) По признаку наличия в кинематических цепях замкнутых контуров цепи могут быть замкнутыми и незамкнутыми; в замкнутой цепи каждое звено входит не менее, чем в две кинематические пары.

Некоторые дополнительные определения:

обобщенная координата механизма – каждая из независимых координат, определяющих положение всех звеньев механизма относительно стойки;

число степеней свободы (степень подвижности) механизма – число независимых вариаций обобщенных координат механизма;

начальное звено – звено, которому приписывается одна или несколько обобщенных координат механизма;

входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев;

выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм.

Примеры.

Методы силового анализа.

Силовой расчет механизмов без учета трения в кинематических парах допускает применение как аналитических, так и графо – аналитических методов.

В настоящем пособии предпочтение отдано графо – аналитическому методу планов сил.

Поскольку векторный план представляет собой графическое изображение векторного равенства, то при простой форме векторных силовых многоугольников их аналитическая обработка достаточно проста и позволяет рассчитать точные силовые соотношения для заданных положений механизмов.

Нагрузки (виды нагрузок, единицы измерения нагрузок).

Нагрузки – это внешние силы, действующие на конструкцию.

Сила – это мера механического воздействия одного тела на другое.

Единица измерения – ньютон (Н).

1Н = 1кг •м/с2

Также приблизительно можно принять:

1кг = 10Н

1кН =1000Н =100кг

1тонна =1000кг =10000Н =10кН

Нагрузки подразделяются:

а) По длительности воздействия – постоянные, временные, переменные.

Б) По характеру приложения – распределённые и сосредоточенные.

В) По характеру воздействия – статические и динамические.

Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.

Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.

Расчетные схемы.

При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.

>Методы и тесты оценки физической работоспособности

Модификация Л.И.Абросимовой

Модификация Л.И.Абросимовой с со-авт.(1978). В настоящее время данный вариант теста используется чаще, Он предусматривает выполнение одной нагрузки. Для получения достаточно точных результатов, сопоставимых с результатами теста в модификации В.Л.Карпмана необходимо подобрать нагрузку, при которой к моменту ее завершения ЧСС достигнет 150-160 уд/мин.
Расчет показателя PWC170 по формуле:
pwc170=w / f — f0 * (170 -f0 )
где:
W — величина нагрузки;
f0 — ЧСС покоя (до нагрузки);
f1 — ЧСС после нагрузки.
Показатели общей физической работоспособности у спортсменов разных видов спорта существенно отличаются, что связано с преимущественным развитием ведущих физических качеств. Наибольшие значения отмечаются у спортсменов, тренирующихся «на выносливость» (длинные и марафонские дистанции).
Таблица 3.4. Оценка физической работоспособности по результатам теста PWC170 (кгм/мин) у квалифицированных спортсменов (модификация Б.Я. карпмана с соавт., 1974)

В тех случаях, когда отсутствует сложная аппаратура или в полевых условиях (на тренировочной базе) тест PWC170 проводят методом степэргометрии.
Определение PWC170 методом степэргометрии. Испытуемый в течение 3 минут совершает подъемы на ступень высотой 35 см с частотой 20 подъемов в минуту (частота метронома 80 ударов в минуту). На один удар метронома совершается одно движение. По окончании нагрузки считают пульс в течение 10 с (P1). Далее выполняется вторая нагрузка с частотой 30 подъемов в минуту (120 уд/мин). По окончанию второй нагрузки снова считают пульс (P2).
Затем определяют показатель PWC170 с помощью таблицы 3.5. На горизонтальной линии находят ЧСС после первой нагрузки, а на вертикальной, соответственно, после второй. Пересечение двух показателей дает величину относительного PWC170 в пересчете на 1 кг веса тела.
Общая работоспособность рассчитывается следующим образом:
PWC170 (кгм/мин) = А * М,
где:
А — величина относительного PWC170 М — масса тела испытуемого.
Таблица 3.5. Определение относительного показателя PWC с помощью данных степ-теста

Таблица 3.6. Оценка результатов теста Новакки

При отсутствии полученной в ходе опыта ЧСС в таблице, величину относительного показателя PWC170 можно найти по формуле:
А=7,2*(1+0,5*(28-Р1)/(Р2-Р1)
где:
P1 — пульс после первой нагрузки; P2 — пульс после второй нагрузки.

Тест Новакки

Тест предусматривает определение времени на протяжении, которого исследуемый способен выполнять нагрузку определенной мощности, которая зависит от массы тела человека. Величина начальной нагрузки составляет 1 Вт/кг. На каждой последующей ступени (ступенчато растущей нагрузки без интервалов отдыха) интенсивность работы постепенно увеличивается на 1 Вт/кг. Длительность каждого этапа составляет 2 минуты. Тест проводится до тех пор, пока исследуемый может выполнять нагрузку или до появления признаков порога толерантности.
При обследовании лиц средних или преклонных лет, а также больных, величина начальной нагрузки должна составлять 1/4 Вт/кг.
Для оценки результатов теста, которая осуществляется с учетом мощности нагрузки и длительности ее удержания, разработана оценочная таблица.
Нормальная физическая работоспособность по данному показателю у нетренированных лиц соответствует — нагрузке мощностью 3 Вт/кг, которая выполнялась в течение 2 мин, а у тренированных — 4 Вт/кг.
Из вышерассмотренных тестов в практике спортивной медицины наиболее часто используют тест PWC170, так как показатели этого теста можно использовать для непрямого определения МПК.

Гарвардский степ-тест

Тест был разработан в Гарвардском университете (США) в 1942 году и является универсальным методом оценки физической работоспособности. Величина индекса Гарвардского степ-теста (ИГСТ) оценивает скорость восстановления пульса после стандартной физической нагрузки.
В состоянии покоя у обследуемого регистрируется пульс за 30 минут и АД. Высоту ступени и время восхождения подбирают, руководствуясь данными табл. 3.7.
Подъем на ступеньку осуществляется с частотой 30 восхождений в 1 мин на протяжении 5 мин. Темп задается метрономом — 120 ударов в минуту. Время восхождения при необходимости может быть ограничено до 2-3 мин. После завершения теста определяется ЧСС в первые 30 сек на 2, 3 и 4-й минутах восстановительного периода. Сразу же после нагрузки регистрируют АД.
Таблица 3.7. Параметры выполнения работы при вычислении ИГСТ

Расчет индекса Гарвардского степ-теста (ИГСТ) выполняется по формуле:
ИГСТ=Т * 100/(f1+f2+f3)*2,
где ИГСТ — в баллах;
Т — время восхождения на ступеньку в сек; f1, f2, f3 пульс за 30 сек на 2, 3 и 4-й минутах восстановления.
Следует учитывать, что общая нагрузка при выполнении данного теста достаточно велика, поэтому его можно использовать лишь здоровым лицам после систематических занятий физкультурой не менее 6 недель.
В табл. 3.8. приводятся оценочные критерии величины Гарвардского степ-теста для здоровых лиц, а в табл. 3.9 в сравнении со спортсменами.
Таблица 3.8. Оценка физической работоспособности по величине ИГСТ

Таблица 3.9. Оценка результатов гарвардского степ-теста у нетренированных и спортсменов разных видов спорта

Сакрут В.Н., Казаков В.Н.

Опубликовал Константин Моканов

кГм

Смотреть что такое «кГм» в других словарях:

• кГм — килограммометр Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. КГМ кварцевая галогенная малогабаритная лампа накаливания КГМ крупногабаритный мусор КГМ … Словарь сокращений и аббревиатур

• кгмін — (гмін) гурт, громада … Зведений словник застарілих та маловживаних слів

• КГм — Килограмм сила метр (кГм) единица энергии и работы МКГСС системы единиц. 1 кГм работа, совершаемая силой 1 кгс при перемещении точки приложения этой силы на расстояние 1 метр по её направлению. 1 кГм = 9,80665 дж. Источники информации Большая… … Википедия

• Кгм — Килограмм сила метр (кГм) единица энергии и работы МКГСС системы единиц. 1 кГм работа, совершаемая силой 1 кгс при перемещении точки приложения этой силы на расстояние 1 метр по её направлению. 1 кГм = 9,80665 дж. Источники информации Большая… … Википедия

• КГМ — (анг. CGM, скр. од computer graphicks metafile графички метафајл) комп. стандарден формат на фајл за запишување на објективно ориентирани графички форми овој стандард е машински независен и овозможува размена на графика меѓу корисници што работат … Macedonian dictionary

• кгм — килограммометр … Словарь сокращений русского языка

• Сбор ТБО (КГМ) — 2.10. Сбор ТБО (КГМ) комплекс мероприятий, связанных с очисткой рабочими комплексной уборки мусорокамер, заполнением контейнеров и зачисткой контейнерных площадок. Сбор КГМ загрузка дворниками и рабочими комплексной уборки бункеров накопителей… … Словарь-справочник терминов нормативно-технической документации

• Вывоз ТБО (КГМ) — 2.11. Вывоз ТБО (КГМ) выгрузка ТБО из контейнеров (загрузка бункеров накопителей с КГМ) в специализированный транспорт, зачистка контейнерных площадок и подъездов к ним от просыпавшегося мусора, и транспортировка их с мест сбора мусора на… … Словарь-справочник терминов нормативно-технической документации

• Договор на вывоз ТБО (КГМ) — 2.12. Договор на вывоз ТБО (КГМ) письменное соглашение, имеющее юридическую силу, заключенное между заказчиком и подрядной мусоровывозящей организацией на вывоз ТБО (КГМ). Источник … Словарь-справочник терминов нормативно-технической документации

• Крупногабаритный мусор (КГМ) — отходы потребления и хозяйственной деятельности (бытовая техника, мебель и др.), утратившие свои потребительские свойства, загрузка которых (по своим размерам и характеру) производится в бункеры накопители… Источник: ПОСТАНОВЛЕНИЕ Правительства … Официальная терминология

• Кажущаяся плотность кгм-3 — 1.2.4. Кажущаяся плотность кгм 3 Обозначение Источник: ГОСТ 4.107 83: Система показателей качества продукции. Порошки огнетушащие. Номенклатура показателей … Словарь-справочник терминов нормативно-технической документации

>Расчет на ударные нагрузки

Теоретические предпосылки расчета

Когда мы рассматривали виды нагрузок, то выяснили, что ударная нагрузка является одним из видов динамических нагрузок и отличается от статической нагрузки тем, что при определении максимальных напряжений следует учитывать силы инерции.

Ударной считается нагрузка, прикладываемая в очень короткий промежуток времени. Например, ударная нагрузка возникает при падении одного тела на другое или при быстром изменении давления между рассматриваемыми телами. Все это кажется довольно странным, ведь если тело, например гиря, имеет массу 32 кг, то масса гири не изменится ни до, ни после, ни в момент падения. И это действительно так, но только тогда, когда речь идет о гравитационной массе, однако тщательное исследование явлений окружающего мира показывает, что у любого тела есть еще и инертная или как ее еще называют — инерционная или инерциальная масса. А еще те же исследования показывают, что инертная масса равна гравитационной массе. Так вот, когда речь идет о ударных нагрузках, то создает такую нагрузку не гравитационная, а инертная масса. В общем курсе физики термин «нагрузка» не используется, а используется понятие «сила». И состояние многих материальных тел описывается взаимодействием различных сил. При этом все силы можно условно разделить на внешние и внутренние. В теоретической механике, теории сопротивления материалов, теории упругости, теории прочности и т.п. внешние силы, действующие на рассматриваемую конструкцию, рассматриваются, как нагрузки, а внутренние силы — как напряжения. При этом предполагается, что сумма внешних сил равна сумме внутренних сил, это в итоге и позволяет составлять уравнения равновесия для рассматриваемой системы.

Когда тело, создающее нагрузку, очень долго взаимодействует с телом, в котором под воздействием этой нагрузки возникают напряжения, то скорость обоих тел, точнее центров тяжести обоих тел, при таком взаимодействии согласно принятой системы отсчета практически не изменяется. Это позволяет рассматривать нагрузку и напряжения, как статические, т.е. обусловленные гравитационным взаимодействием. При ударе в зависимости от массы соударяемых тел, скорость одного из тел или обоих тел изменяется очень сильно и в сравнительно короткий промежуток времени. Одной из характеристик тела, двигающегося с некоторой скоростью, является импульс:

p = mиv (288.1)

В данном случае в виду имеется именно инертная масса, и рассматривается поступательное (прямолинейное) движение, т.е. такое движение, для корректного описания которого достаточно рассматривать движение только одной материальной точки, совпадающей с центром тяжести рассматриваемого тела. Для характеристики вращательного движения используются понятия момента инерции и угловой скорости, для сложного движения материальных точек изгибаемой конструкции — коэффициент жесткости, определяющий характер движения различных материальных точек, входящих в состав изгибаемой конструкции в зависимости от значений момента инерции, модуля упругости материала, действующей нагрузки и длины изгибаемой конструкции.

Когда тела сталкиваются с относительно большой скоростью, то из-за изменения скорости в течение короткого промежутка времени возникает ударная сила, точнее две ударные силы, одинаковые по значению и направленные противоположно. Таким образом рассматриваемая система сил по прежнему остается в равновесии:

Рисунок 1. Равновесие сил рассматриваемой системы.

Если рассматривать тело, создавшее ударную нагрузку, то на него будет действовать ударная сила, равная сумме опорных реакций, показанных на рисунке 1.б) и равная — Qу, т.е. направленная противоположно. Однако строителей очень редко интересует судьба падшего тела, им необходимо обеспечить прочность конструкции после удара, т.е. рассчитываемая конструкция должна работать только в области упругих, восстанавливаемых со временем деформаций, а неупругие деформации, могут привести к разрушению конструкции.

Теоретически, если известно время t, в течение которого импульс будет передаваться от одного тела другому, определить ударную силу не проблема, так как

Qу = mиv/t (288.2)

и тогда расчет конструкции можно просто выполнить на действие ударной силы, т.е. по расчетной схеме, показанной на рисунке 1.б). Да вот беда, время, в течение которого импульс передается от одного тела другому, зависит от множества различных факторов (о которых речь ниже) и может измеряться в пределах от микросекунд до секунд. Потому точно определить значение времени, а значит и ударной силы достаточно сложно.

Далее, в процессе удара кинетическая энергия упавшего тела частично трансформируется в потенциальную энергию деформации рассматриваемой конструкции. Например балка, показанная на рисунке 1, прогнется, при этом в момент, когда значение деформации, будет максимальным, скорость движения центра тяжести балки будет равной нулю, а значит систему можно рассматривать как статическую. Вот только упавшее тело, если оно все еще находится на балке, уже не будет создавать ударную нагрузку, а только обычную статическую, поэтому внутренние напряжения начнут уменьшаться, а значит, и величина деформации будет уменьшаться. А в результате действия инерциальных сил, возникающих как при движении груза, так и при движении частиц рассматриваемой конструкции такое движение превратится в колебательное, со временем затухающее из-за перехода части кинетической и потенциальной энергии в тепловую.

Кроме того часть энергии удара преобразуется в звуковые колебания и если верить индийским фильмам, то в звук преобразуется чуть ли не вся энергия удара. Так же при ударе часть энергии переходит в упругие и неупругие деформации падающего тела и местные неупругие деформации рассматриваемого элемента конструкции, а потому точное решение задачи о возникающих при ударе внутренних напряжениях и деформациях материала конструкции с учетом вышеприведенных факторов является не простой задачей. Однако в точном решении задач не всегда есть необходимость и потому в строительной практике получили распространение приближенные методы расчета.

Максимально упростить решение подобных задач помогают следующие допущения и физические модели процесса:

1. Любую балку, плиту, стену, колонну или другую строительную конструкцию можно рассматривать как упругую систему с одной степенью свободы. Этим подразумевается, все деформации будут находиться в области упругих, т.е. восстанавливаемых со временем и то, что колебания будут происходить только относительно одной из осей. Например, при падении тела на рассматриваемую конструкцию под действием силы тяжести перемещение падающего тела происходит только вдоль оси у, возможные смещения тела вдоль осей х и z не учитываются. Некая тело с массой m, соединенное с упругой пружиной, является простейшей линейной механической моделью упругой системы с одной степенью свободы:

Рисунок 2. Амплитуда колебаний

2. Амплитуда колебаний, определяющая максимальное отклонение рассматриваемой точки вдоль оси у, соответствует максимальной деформации рассматриваемой конструкции. При продольном ударе — это относительное изменение длины Δl, при изгибающем ударе — прогиб f, при вращающем ударе — угол поворота φ (далее мы будем рассматривать в основном изгибающий удар). При рассмотрении колебательного движения физических тел, двигающихся по прямолинейной траектории, рассматриваемая точка, совершающая колебания, соответствует центру тяжести тела, если масса изгибаемой конструкции пренебрежимо мала, по сравнению с массой ударяющего тела, то для упрощения расчетов массой изгибаемой конструкции можно пренебречь и рассматривать колебания согласно принятой физической модели (рисунок 2).

3. Так как колебания системы, вызванные ударом, являются затухающими из-за сопротивления окружающей среды (как минимум воздуха) и наличия сил внутреннего трения, постепенно переводящих часть энергии удара в нагрев, то максимальная амплитуда, соответствующая максимальной деформации, будет только в течение первого периода колебания. Таким образом расчет сводится к определению максимально возможной амплитуды в течение первого периода колебания.

4. Деформации рассматриваемого элемента конструкции от ударяющего тела распространяются по всей длине элемента, подчиняются закону Гука и пропорциональны деформациям, которые возникают при статическом приложении нагрузки от того же тела и в том же месте, т.е. расчетные схемы, показанные на рисунке 1, могут использоваться для расчета рассматриваемой конструкции.

5. Пропорциональность динамических и статических деформаций δ определяется динамическим коэффициентом удара kд, соответственно пропорциональность динамических и статических напряжений σ также определяется динамическим коэффициентом:

δд = kдδст (288.3.1)

σд = kдσст (288.3.2)

соответственно

Qд = kдQст (288.3.3)

Мд = kдМст (288.3.4)

и так далее.

6. Предполагается, что падающее тело имеет жесткость значительно больше жесткости рассматриваемого элемента конструкции. Это позволяет не учитывать величину упругих деформаций падающего тела при ударе и соответственно исключает развитие неупругих деформаций в упавшем теле. Соответственно время, в течение которого импульс от одного тела передается другому будет минимальным, а значит и значение ударной силы будет максимально возможным. И даже если на железную балку падает железная гиря, имеющая вполне определенную жесткость, то для упрощения расчетов упругие и возможные неупругие деформации гири не учитываются. Результат такого допущения — дополнительный запас по прочности.

7. Предполагается, что падающее тело с момента прикосновения к рассматриваемому элементу конструкции продолжает движение с такой же скоростью, с какой перемещается поперечное сечение элемента под телом в результате развития деформаций, т.е. упавшее тело как бы прилепляется к рассматриваемому элементу и не отскакивает до момента развития максимальных деформаций. Такое допущение справедливо лишь тогда, когда масса упавшего тела не меньше массы элемента. А если масса рассматриваемого элемента пренебрежимо мала по сравнению с массой падающего тела, то в момент столкновения изменением скорости вообще можно пренебречь и рассматривать изменение скорости упавшего тела после столкновения только как результат изменения потенциальной энергии деформации и тогда принятая физическая модель будет наиболее полно соответствовать реальному процессу. Если масса рассматриваемого элемента равна или больше массы падающего тела, то такое допущение также приводит к дополнительному запасу по прочности.

8. Явление удара рассматривается с позиций закона сохранения энергии и соответственно сохранения импульсов. При этом предполагается, что кинетическая энергия Т1 падающего тела — груза в момент удара полностью превращается в потенциальную энергию Uд2 деформации конструкции и кинетическую энергию Т’2 движения рассматриваемой конструкции:

Е = Т1 = Uд2 + Т’2 (288.4.1)

Это допущение справедливо только при рассмотрении столкновения двух равноупругих тел имеющих равную массу, при этом одно из тел до момента столкновения находится в состоянии покоя, т.е. его скорость равна нулю. Поэтому количество кинетической энергии рассматриваемой конструкции Т2 принимается равным нулю, а также принимается равным нулю количество кинетической энергии Т’1 падающего тела сразу после момента столкновения, так как скорость падающего тела в момент столкновения обнуляется.

Если масса рассматриваемого элемента конструкции пренебрежимо мала по сравнению с массой ударяющего тела, то величиной Т2 для упрощения расчетов можно пренебречь и рассматривать изменение кинетической энергии падающего тела как изменение потенциальной энергии деформации рассматриваемого элемента:

Т = Uд (288.4.2)

Это допущение, не учитывающее переход части энергии в звуковую, тепловую и другие воды энергии также дает дополнительный запас по прочности.

Принятие этих допущений позволяет значительно упростить расчет конструкций и даже обеспечить дополнительный запас по прочности для колонны, стойки, балки, плиты и любого другого рассматриваемого элемента конструкции при использовании физической модели, показанной на рисунке 2.

В зависимости от направления удара по отношению к оси рассматриваемого элемента конструкции и характера происходящих деформаций удары рассматриваются как продольный — приводящий к растяжению или сжатию рассматриваемого элемента (колон, стоек, стен, свай), поперечный — вызывающий деформации изгиба (поперечный удар часто называют изгибающим ударом) характерен для стержней, балок, плит перекрытия, и крутильный удар — вызывающий деформации кручения в валах машин и механизмов или в балках при внецентренном приложении ударной нагрузки.

Теория расчета на динамическую нагрузку

Согласно основному закону динамики — второму закону Ньютона — любое тело, имеющее некоторую массу m и движущееся с ускорением свободного падения g = 9.81 м/с2, может рассматриваться как сила Q = mg, а при расчете строительных конструкций внешние силы, как уже говорилось, рассматриваются, как нагрузка. Именно поэтому в формулировке задач по расчету строительных конструкций нагрузки от тел, имеющих некоторую массу m, измеряемую в понятных простому человеку килограммах или тоннах , указываются в не столь хорошо известных и понятных Ньютонах и килоНьютонах. Теоретически это правильно, но вполне допустимо при выполнении расчетов заменять Ньютоны на килограмм-силы. Например, человека весом в 100 кг, можно рассматривать как сосредоточенную нагрузку Q = 1000 Н = 100 кгс или просто 100 кг. При этом уменьшение значения, возникающее при умножении массы на 9.81 обычно не учитывается, что опять таки приводит к дополнительному запасу по прочности.

При этом даже если человек стоит абсолютно неподвижно в течение долгого времени, т.е. скорость его перемещения в рассматриваемой системе отсчета равна нулю, то он все равно создает нагрузку, в данном случае статическую. Этот парадокс устраняется тем, что если опору из под человека убрать, то он полетит к центру Земли, причем с ускорением, мало отличающимся от ускорения свободного падения и значит опора может рассматриваться как такая же сила, только действующая в противоположную сторону, и называется эта сила опорной реакцией. А когда опорная реакция равна опорной силе, то система находится в состоянии равновесия, т.е. никуда не движется (во всяком случае в принятой системе отсчета). При рассмотрении стержней и балок, имеющих две опоры, таких опорных реакций будет две (см. рисунок 1).

Однако все это справедливо только для абсолютно жестких тел. Реальные же тела и в частности строительные конструкции под воздействием нагрузки деформируются, а значит и человек, представляющий собой нагрузку, будет перемещаться в пространстве на величину этой деформации.

Как определяются деформации для сжатых, растянутых и изгибаемых элементов, и при чем тут момент инерции, мы уже знаем, осталось только добавить, что при расчете деформаций от действия статической нагрузки предполагается, что статическая нагрузка прикладывается не моментально, а очень медленно, т.е. значение нагрузки постепенно нарастает от нуля до максимального значения за время, значительно превышающее время деформации. Таким образом скорость перемещения в пространстве тела, создающего нагрузку, стремится к нулю и получается, что наблюдаемые в результате воздействия нагрузки деформации, например вот такие:

Фотография 174.1. Прогиб балки — линейки при действии статической нагрузки — мерного стакана

это результат действия только гравитационной массы тела, создающего нагрузку. Дальнейшее описание будет производиться на примере балки линейки для наглядности.

Если приложить нагрузку мгновенно, например, если поставить мерный стакан на линейку и сразу его отпустить, то прогиб будет значительно больше. Потому что стакан, опускаясь вместе с прогибающейся линейкой, на определенном этапе приобретет достаточно большую скорость, а значит, при расчетах нужно учитывать не только гравитационную, но и инертную массу тела, а также инертную массу рассматриваемой конструкции. Так как физиками до сих пор считается, что гравитационная масса равна инертной (во всяком случае попытки опровергнуть это утверждение пока ни к чему не привели), то вполне логично предположить, что инертная масса приведет к такой же деформации как и гравитационная масса, а значит деформация от динамической нагрузки будет в 2 раза больше, чем от статической нагрузки, создаваемой тем же телом. В математическом выражении это предположение с учетом теоретических предпосылок (т.е. без учета массы линейки) выглядит так:

— для статической нагрузки kд = 1

— для динамической нагрузки kд = 1 + 1 = 2

Впрочем, такой метод определения динамического коэффициента при мгновенном приложении нагрузки может показаться слишком простым. Что ж, устранить эту проблему не сложно. Для начала вернемся к п.2 и 3 теоретических предпосылок и рассмотрим их более детально.

В общем виде уравнение гармонических колебаний, позволяющее определить значение отклонения по оси у — что в нашем случае соответствует величине деформации f, выглядит так:

Рисунок 3. Амплитуда колебаний, как радиус окружности и гипотенуза прямоугольного треугольника

у = Аsinφ = Asin(φo + ωt) (288.5.1)

где φ = φo + ωt — фаза колебания, соответственно φo — начальная фаза колебания при t =0.

При этом амплитуда рассматривается, как радиус окружности, а фаза колебаний, как угол наклона этого радиуса, что в итоге и дает нам синусоиду для исследуемой точки, показанную на рисунке 2. Так как скорость материальной точки является производной расстояния по времени, то

y’ = v = (Asin((φo + ωt))’ = Aωcos(φo + ωt) (288.5.2)

тогда значение амплитуды по оси х можно рассматривать как t = v/ω. Ну а дальше из установленных Архимедом соотношений сторон прямоугольного треугольника, образованного катетами х и у и гипотенузой А, следует, что:

А = √¯(у2 + х2) = √¯(у2 + (v/ω)2) (288.5.3)

Если придать этой легкой математической формуле тяжелый физический смысл, то получается, что максимальное значение отклонения по оси у, а в нашем случае величина деформации f, будет максимальным, когда скорость материальной точки — стакана будет равна нулю и соответственно максимальная скорость у материальной точки будет в моменты, когда деформация будет равна нулю. Причина этого — в воздействии сил инерции. Так как нас интересует только максимальное значение отклонения, равное амплитуде, т.е. у = А, т.е. при скорости материальной точки, равной нулю, то формулу (288.5.3) можно с учетом этого преобразовать в:

А = √‾(yи2) (288.5.4)

где уи — максимальное значение деформации при действии сил инерции. При этом полное значение деформации с учетом действия гравитационных сил (на примере линейки) составит:

fп = fг + fи = 2fг = 2fи = fг + √¯(fг2) (288.6.1)

Так как прогиб от действия инертной массы равен прогибу от действия гравитационной массы.

Соответственно динамический коэффициент составит

kд = 1 + 1 = 1 + √¯(12) = 2 (288.6.2)

Если вернуться к математической модели, то мы как бы смещаем вниз по оси у синусоиду (рисунок 2) или окружность (рисунок 3) на значение уг, равное уи, и таким образом получаем полное значение деформации в точках экстремума функции.

Таким образом человек, который ходит по помещению и при этом достаточно быстро перебирает ногами, перенося свой вес с одной ноги на другую, создает как минимум динамическую нагрузку и потому при расчете конструкций перекрытия на нагрузку от такого человека статическую нагрузку, создаваемую гравитационной массой человека, следует умножать на динамический коэффициент kд = 2. При этом высота падения и соответственно скорость падения в момент столкновения принимаются равными нулю.

Теория расчета на ударную нагрузку

До этого мы рассматривали деформацию тела (балки) под действием динамической нагрузки, т.е. в ситуации, когда скорость груза в момент касания с конструкцией равна нулю. Если же груз будет падать с некоторой высоты, то в момент касания с конструкцией эта скорость не будет равна нулю (при принятой нами массе балки значительно меньшей, чем масса груза) и тогда для определения амплитуды теоретически можно использовать формулу (288.3.3). Вот только для этого придется сначала определить значение скорости в момент удара.

Скорость тела, падающего с ускорением свободного падения, без учета влияния сопротивления окружающей среды в любой момент времени можно определить по формуле:

v = √¯(vo2 + 2gh) (288.7.1)

где h — высота падения, м.

Если начальная скорость vo = 0, то формула (288.6.1) примет вид

v = √(2gh) (288.7.2)

Теперь попробуем определить значение циклической частоты ω (или угловой скорости — это кому как больше нравится). Так как ускорение — это вторая производная расстояния по времени, то:

y» = a = (Asin((φo + ωt))» = — Aω2sin(φo + ωt) (288.8)

Физический смысл этой формулы в том, что ускорение движения тела а, подобно скорости v и величине смещения y, подчиняется гармоническому закону, но колебания ускорения на полпериода (на угол П) расходятся с колебаниями смещения и находятся как бы в противофазе смещению. То есть когда смещение (в нашем случае прогиб f) максимально, то ускорение а также максимально, но направлено в сторону, противоположную смещению. Так же здесь заметим, что колебания скорости смещены на четверть периода или на угол П/2, по отношению к колебаниям смещения.

Таким образом из формул (288.3.1) и (288.7) можно вывести уравнение гармонических колебаний:

a/ω2 + y = 0 или у» + ω2y = 0 (288.9)

соответственно

ω2 = — или ω2 = Q/my = g/yи (288.10.1)

В данном случае имеется в виду инертная масса груза, а масса балки не учитывается. Тогда согласно формул (288.5.3), (288.7.2) и (288.10.1)

у = √¯(уи2 + 2ghyи/g) = √¯(уг2 + 2hyг) (288.11.1)

Тогда полное значение деформации составит:

уп = уг + √¯(уг2 + 2hyг) (288.11.2)

тогда

kд = уп/уг = 1 + √1 + 2h/yг = 1 + √1 + 2h/уст (288.11.3)

Как правило никакой разницы между деформациями от динамической и ударной нагрузки не делается, а динамическая нагрузка рассматривается как частный случай ударной нагрузки, при которой скорость падающего груза в момент контакта с рассматриваемой конструкцией равна нулю, понятие «ударный коэффициент» — не используется, величина деформации от действия гравитационной массы обозначается как статическая деформация уст. Сути дела это не меняет, но упомянуть об этом стоит, равно как и о том, что формулы (288.11) можно вывести и другими способами. Здесь же приведен, возможно и не самый простой, но по моему мнению самый наглядный способ. И еще, если присмотреться, то формулы для определения скорости, вертикального смещения, и многих других не приведенных здесь параметров, достаточно похожи, а роднит их принцип определения гипотенузы прямоугольного треугольника. Вот такие дела.

Если вернуться к математической модели, то при определении амплитуды при ударной нагрузке мы рассматривали как бы не всю, а только нижнюю часть синусоиды, при этом амплитуда рассматриваемой синусоиды соответствует амплитуде колебаний, создаваемой при динамической нагрузке грузом, имеющим массу, умноженную на динамический коэффициент.

Для упрощения расчетов при h/yст > 10 единицей в подкоренном выражении можно пренебречь и тогда формула (288.11.3) примет вид:

kд = 1 + √2h/уст (288.11.4)

А если h/yст > 100, то можно не учитывать и единицу перед квадратным корнем, тогда:

kд = √2h/уст (288.11.5)

Пример расчета балки на ударную нагрузку

Имеется шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На средину балки с высоты 50 см падает гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.

1. Определим прогиб балки при воздействии статической нагрузки

fcт = Ql3/48EI = 32х4003/(48х100000х6666.667) = 0.064 см

где Е = 105 кгс/см2 — модуль упругости древесины, I = bh3/12 = 6666.667 см4 — момент инерции поперечного сечения.

2. Если определять динамический коэффициент с учетом того, что высота падения значительно больше статического прогиба, то

kд = 1 + √(2х50/0.064) = 40.53

3. Тогда максимальный прогиб составит

fд = 0.064х40.53 = 2.59 см

4. Это достаточно большой прогиб, но намного важнее выяснить, выдержит ли такую ударную нагрузку балка

Мд = Qlkд/4 = 32х400х40.53/4 = 129696 кг·см

5. Тогда при расчетном сопротивлении R = 140 кг/см2 требуемый момент сопротивления составит

Wтр = М/R = 129696/140 = 926.4 см3

6. Момент сопротивления для балки сечением 20х10 см составит W = 2I/h = 6666.667/10 = 666.67см3 < Wтр = 926.4 см3.

Вывод: балка под действием такой ударной нагрузки разрушится.

Пример расчета балки на ударную нагрузку от груза, падающего не посредине балки

Имеется все та же шарнирно закрепленная балка перекрытия длиной 4 м из древесины сечением 20х10 см. На расстоянии 1 м от опоры балки с той же высоты 50 см падает все та же гиря весом в 32 кг. Требуется определить прочность балки при ударной нагрузке.

1. Определим прогиб балки в месте падения груза при воздействии статической нагрузки

fcт = Qа2b2/3lEI = 32х1002×3002/(3х400×100000х6666.667) = 0.036 см

kд = √2х50/0.036 = 52.7

как видим, за счет смещения места падения груза к одной из опор динамический коэффициент даже увеличился, но нас по прежнему интересует прочность балки

Мд = Qabkд/l = 32х100×300х52.7/400 = 126491 кг·см

так как максимальное значение изгибающего момента почти не изменилось, то и без дальнейших расчетов понятно, что балка такую ударную нагрузку не выдержит. А вот если груз упадет очень близко к одной из опор, например на расстоянии 10 см, то

fcт = Qа2b2/3lEI = 32х102×3902/(3х400×100000х6666.667) = 0.00061 см

kд = √2х50/0.00061 = 405.42

Мд = Qabkд/l = 32х10×390х229.4/400 = 126491 кг·см

Вывод: на каком бы расстоянии от опоры ни упал груз, балка под действием такой ударной нагрузки разрушится.

Пример расчета балки на ударную нагрузку с учетом жесткости падающего груза

Как видим, если рассматривать соударение балки с гирей, как абсолютно жестким телом, то у балки никаких шансов на выживание нет, она разрушится. Однако любое физическое тело имеет вполне определенную жесткость, а это значит, что такое тело будет также деформироваться. А значит, время контакта при столкновении двух тел из-за упругих и возможных неупругих деформаций ударяющего тела будет больше и соответственно ударная сила, действующая на балку, будет меньше. Это подтверждают эксперименты со сталкивающимися телами из любых материалов. Например, когда относительно легкий стальной шарик падает на очень массивную стальную пластину, то теоретически после соударения относительно легкий металлический шарик должен отскочить от очень массивной пластины на высоту, примерно равную высоте, с которой шарик упал. Однако в реальности высота отскока значительно меньше, и разница доходит до 3 раз. На основании этого можно определить коэффициент восстановления:

kв = √h’/h (288.12)

где h’ — высота отскока, а h — высота падения.

Этот коэффициент будет показывать, насколько уменьшится ударная сила с учетом упругих свойств падающего груза и тогда

kуд = 1 + √1 +2h’/fстили kyд = kдkв (288.13)

ниже приведены значения коэффициента восстановления для некоторых веществ:

Таблица 1. Коэффициенты восстановления при частично упругом соударении тел

Вещество	k
Древесина	0.5
Пробка	0.55
Сталь	0.55
Слоновая кость	0.889
Стекло	0.9375

Помимо всего прочего изучение этой таблицы позволяет понять, почему раньше для изготовления бильярдных шаров использовалась именно слоновая кость. Но в данном случае нас интересует сталь, точнее гиря изготовленная с применением железа. Конечно же на значение коэффициента восстановления будет влиять геометрическая форма падающего тела, и чем ближе эта форма к шару тем ближе значение коэффициента восстановления к указанному в таблице. Поэтому значение коэффициента восстановления следует дополнительно умножить на поправочный коэффициент kп = 0.5 — 1, учитывающий форму падающего тела в зависимости от материала сталкивающихся тел. Определение более точного значения поправочного коэффициента — отдельная большая тема. Однако для упрощения расчетов лучше не уменьшать значение коэффициента восстановления, а наоборот увеличить, умножив на коэффициент надежности по нагрузке γ = 1.1 — 1.3.

Например, при столкновении железной гири с деревянной балкой можно использовать коэффициент γ = 1.2 и тогда:

kд = 40.53х0.55х1.2 = 26.75

тогда максимальный прогиб составит

fд = 0.064х26.75 = 1.71 см

Мд = Qlkд/4 = 32х400х26.75/4 = 85600 кг·см

Wтр = М/R = 85600/140 = 611.4 см3

момент сопротивления W = 6666.667/10 = 666.67см3 > Wтр = 611.4 см3.

Вывод: балка выдержит такую ударную нагрузку, однако существует очень высокая вероятность того, что после удара на поверхности балки останется порядочная вмятина, а выражаясь научным языком, изменятся размеры поперечного сечения балки, что приведет к изменению несущей способности балки. Поэтому даже если балка и выдержит один удар, то нет никакой гарантии, что балка выдержит много ударов и такую балку желательно избавить от такого насилия. Обычно это происходит по умолчанию, когда на балки перекрытия укладываются доски напольного покрытия. И тогда в результате падения тяжелых грузов с относительно большой высоты будет страдать уже не балка, а точнее не только балка, но и доски, а если это доски чернового пола, то покрытие по черновому полу. А потому обычно выполняется дополнительная защита пола в местах, где падение груза на перекрытие достаточно вероятно. Принцип такой защиты прост — чем толще защитное покрытие и чем меньше модуль упругости материала защитного покрытия, тем меньше будет в итоге ударная сила, действующая на конструкции перекрытия. Да и поменять защитное покрытие намного быстрее и дешевле, чем балки или плиты перекрытия.

Кстати на эффекте развития местных неупругих деформаций основаны различные методы неразрушающих методов определения прочности бетона, в частности для этого может использоваться молоток Кашкарова, но это уже совсем другая тема.

И еще, борцы тоже не любят бороться на жестком бетонном полу, а все больше на специальных покрытиях и вовсе не потому, что заботятся о надежности перекрытия, в этом случае за основу берется прочность главной несущей конструкции человеческого организма — скелета и в частности черепа.

Динамические нагрузки

Динамическая нагрузка — нагрузка, характеризующаяся быстрым изменением во времени её значения, направления или точки приложения и вызывающая в элементах конструкции значительные силы инерции. Динамические нагрузки испытывают детали машин ударного действия, таких, как прессы, молоты и т. д. Детали кривошипно-шатунных механизмов также испытывают во время работы значительные динамические нагрузки от изменения величины и направления скоростей, то есть наличия ускорений. К динамическим нагрузкам относят и ударные нагрузки. При проектировании частей конструкции, находящихся под действием ударной или вибрационной нагрузки от станков, двигателей, молотов и т.д., производят расчёт на действие динамической нагрузки. Для устранения динамических нагрузок их снижают или ограничивают, например, при помощи электропривода, тормозных устройств и других механизмов.

Статическая нагрузка — нагрузка, величина, направление и точка приложения которой изменяются во времени незначительно. При прочностных расчетах можно пренебречь влиянием сил инерции, обусловленных такой нагрузкой. Статической нагрузкой, например, является вес сооружения.

Запас устойчивости — отношение той нагрузки, при которой деталь или конструкция теряет устойчивость (прочность (см. предел прочности), эластичность, упругость, пластичность), к фактической или вычисленной нагрузке; представляет собой безразмерную величину.

Примечания

• Пиковые нагрузки в общественном транспорте

Это заготовка статьи по механике. Вы можете помочь проекту, дополнив её.

Физическая динамическая нагрузка

1. Физическая динамическая нагрузка выражается в единицах внешней механической работы за смену (кг — м).

Для подсчета физической динамической нагрузки (внешней меха­нической работы) определяется масса груза, перемещаемого вручную в ‘ каждой операции и путь его перемещения в метрах. Подсчитывается общее количество операций по переносу груза за смену и суммируется величина внешней механической работы (кг • м) за смену в целом. По величине внешней механической работы за смену в зависимости от вида нагрузки (региональная или общая) и расстояния перемещения груза определяют, к какому классу условий труда относится данная работа. Если расстояние перемещения груза разное, то суммарная механическая работа сопоставляется со средним расстоянием перемещения

Пример. Рабочий (мужчина) поворачивается, берет с конвейера деталь (масса 2,5 кг), перемещает ее на свой рабочий стол (расстояние 0,8 м), выполняет необходимые операции, перемещает деталь обратно на конвейер и берет следующую, Всего за смену рабочий обрабатывает 1200 деталей. Для расчета внешней механической работы вес деталей умножаем на расстояние перемещения и еще на 2, т. к каждую деталь рабочий перемещает дважды (на стая и обратно), а затем на количество деталей за смену. Итого:2,5кг- 0.8м — 2 • 1200 -4800кгм. Работа региональная, расстояние перемещения груза до 1 м, следовательно, по показателю 1.1 работа относится ко 2 классу.

Масса поднимаемого и перемещаемого груза вручную

Для определения массы (кг) груза (поднимаемого или переносимо­го рабочими на протяжении смены, постоянно или при чередовании с другой работой) его взвешивают на товарных весах. Регистрируется только максимальная величина. Массу груза можно также определить по документам. Для определения суммарной массы груза, перемещае­мого в течение каждого часа смены, вес всех грузов суммируется, а если переносимый груз одного веса, то этот вес умножается на число подъе­мов или перемещений в течение каждого часа.

Пример. Рассмотрим предыдущий пример. Масса груза 2,5 кг, следовательно, по п. 2.2 можно отнести к 1 классу. За смену рабочий поднимает /200 деталей, по 2 раза каждую. В час он перемещает 150 деталей (1200 деталей :8ч). Каждую деталь рабочий берет в руки 2 раза, следовательно, суммарная масса груза, перемещаемая в течение каждого часа смены, составляет 750 кг (150 • 2,5 кг ■ 2). Груз пере­мещается с рабочей поверхности, поэтому эту работу по п.2.3 мож­но отнести ко 2 классу.

Стереотипные рабочие движения (количество за смену)

Понятие «рабочее движение» в данном случае подразумевает движение элементарное, т. е. однократное перемещение тела или части тела из одного положения в другое. Стереотипные рабочие движения в зависимости от нагрузки делятся на локальные и региональные. Ра­боты, для которых характерны локальные движения, как правило, выполняются в быстром темпе (60—250 движений в мин), и за смену количество движений может достигать нескольких десятков тысяч. Поскольку при этих работах темп, т. е. количество движений в едини­цу времени, практически не меняется, то, подсчитав, вручную или с применением какого-либо автоматического счетчика, число движений за 10—15 мин, рассчитываем число движений в 1 мин, а затем умножа­ем на число минут, в течение которых выполняется эта работа. Время выполнения работы определяем путем хронометражных наблюдений или по фотографии рабочего дня. Число движений можно определить также по дневной выработке.

Пример. Оператор ввода данных в персональный компьютер вы­полняет за смену около 55000 движений. Следовательно, по п. 3.1 его работу молено отнести к классу 5.1.

Региональные рабочие движения выполняются, как правило, в бо­лее медленном темпе и легко подсчитать их количество за 10—15 мин или за 1—2 повторяемые операции, несколько раз за смену. После это­го, зная общее количество операций или время выполнения работы, подсчитываем общее количество региональных движений за смену.

Пример. Маляр выполняет около 120 движений большой амплиту­ды в минуту. Всего основная работа занимает 65 % рабочего времени, т. е, 312 мин за смену. Количество движений за смену — 37440 (312 • 120), что по п. 3.2 позволяет отнести его работу к классу 3.2.

Статическая нагрузка

(величина статической нагрузки за смену при удержании груза, приложении усилий, кгс-с)

Статическая нагрузка, связанная с поддержанием человеком гру­за или приложением усилия без перемещения тела или его отдельных звеньев, рассчитывается путем перемножения двух параметров: вели­чины удерживаемого усилия и времени его удерживания.

В производственных условиях статические усилия встречаются в двух видах: удержание обрабатываемого изделия (инструмента) и прижим обрабатываемого инструмента (изделия) к обрабатываемому изделию (инструменту). В первом случае величина статического уси­лия определяется весом удерживаемого изделия (инструмента). Вес изделия определяется путем взвешивания на весах. Во втором случае величина усилия прижима может быть определена с помощью тензометрических, пьезокристаллических или каких-либо других датчиков, которые необходимо закрепить на инструменте или изделии. Время удерживания статического усилия определяется на основании хроно­метражных измерений (по фотографии рабочего дня).

Пример. Маляр (женщина) промышленных изделий при окраске удерживает в руке краскопульт весом 1,8 кгс, в течение 80 % времени сме­ны, т.е. 23040 секунд. Величина статической нагрузки будет составлять 41427 кгс-с (1,8 кгс 23040 с). Работа по п. 4 относится к классу 3.1.

Рабочая поза

Характер рабочей позы (свободная, неудобная, фиксированная, вынужденная) определяется визуально. Время пребывания в вынуж­денной позе, позе с наклоном корпуса или другой рабочей позе, оп­ределяется на основании хронометражных данных за смену.

Пример. Врач-лаборант около 40 % рабочего времени проводит в фиксированной позе — работает с микроскопом. По этому пункту его работу можно отнести к классу 3. 1.

6. Наклоны корпуса(количество за смену)

Число наклонов за смену определяется путем их прямого под­счета или определением их количества за одну операцию и умножа­ется на число операций за смену. Глубина наклонов корпуса (в гра­дусах) измеряется с помощью любого простого приспособления для измерения углов (например, транспортира).

Пример. Для того чтобы взять детали из контейнера, стоящего на полу, работница совершает за смену до 200 глубоких наклонов (более 30°). По этому показателю труд относится к классу 3.1.

Перемещение в пространстве

(переходы, обусловленные технологическим процессом в течение смены по горизонтали или вертикали — по лестницам, пандусам и др., км)

Самый простой способ определения этой величины — с помощью шагомера, который можно поместить в карман работающего или за­крепить на его поясе, определить количество шагов за смену (во время регламентированных перерывов и обеденного перерыва шагомер снимать). Количество шагов за смену умножить на длину шага (муж­ской шаг в производственной обстановке в среднем равняется 0,6 м, а женский — 0,5 м), и полученную величину выразить в км.

Пример. По показателям шагомера работница при обслуживании станков делает около 12000 шагов за смену. Проходимое ею рас­стояние составляет 6000 м или 6 км (12000 • 0,5 м). По этому пока­зателю тяжесть труда относится ко второму классу.

Сердце и физические нагрузки

О том, что подвижный образ жизни, занятия физкультурой и дозированные физические нагрузки положительно влияют на наше сердце, слышали, конечно, все, также как и о призыве «Бегом от инфаркта». Однако в последнее время взгляды на то, «что такое хорошо, и что такое плохо» в отношении физических нагрузок при сердечно-сосудистых заболеваниях, несколько трансформировались.

Физическая реабилитация пациентов занимает важное место в комплексном лечении больных с ишемической болезнью сердца, гипертонической болезнью и хронической сердечной недостаточностью. Главное отличие от принципов, провозглашавшихся 10 – 15 лет назад, заключается в том, что сегодня этой категории пациентов рекомендуется строго дозироаванная легкая физическая нагрузка: ходьба, плавание, велотренинг. Посещение же спортивных залов, занятия на тренажерах, «бег от инфаркта» и прочие тяжелые физические нагрузки не допускаются.

Виды физических нагрузок

Физические нагрузки разделяются на три вида: статистические, динамические и «взрывные».

Статические нагрузки

Статическими называют нагрузки, при которых преобладает длительное напряжение отдельных групп мышц, например, вынужденная поза во время работы.

При статических или изометрических нагрузках происходит напряжение мышц без их укорочения или удлинения. Т.е. мышцы напряжены, но никакой внешней работы не наблюдается, в них идет активный расход энергии и накопление продуктов этого распада, в первую очередь, молочной кислоты. Кровеносные сосуды при статических нагрузках стиснуты напрягшимися мышцами, сердцу приходится проталкивать кровь через сосуды, длительно сдавленные напряженными мышцами. Нарушается не только приток, но и отток крови — ухудшается удаление вредных продуктов распада энергетических структур, жидкость застаивается в тканях и клетках, нарушая их естественный обмен веществ. Происходит выброс гормонов и гормоноподобных веществ, которые значительно повышают давление, увеличивают нагрузку на сердце.

Изометрические нагрузки и работа, связанная с длительным статическим напряжением, категорически противопоказана больным стенокардией, перенесшим инфаркт миокарда и воспалительные заболевания миокарда, а также лицам, имеющим признаки сердечной недостаточности.

«Взрывные» нагрузки

«Взрывные» нагрузки характеризуются очень сильным и коротким напряжением мышц, например, при подъеме тяжестей.

Взрывные нагрузки по своему воздействию на сердце являются самыми неблагоприятными. Предъявляемые требования к сердцу при этом заключаются в необходимости обеспечения значительного мышечного напряжения (например, при поднятии штанги) и сочетают в себе как механизм статического напряжения, когда нарушается кровоток в напряженных мышцах, так и механизм динамического выполнения работы, когда усиленное сокращение мышц вызывает лавинообразный расход энергии и уменьшение содержания энергоаккумулирующих веществ (например, АТФ).

Даже несмотря на кратковременность «взрывных» нагрузок, сердце испытывает серьезную перегрузку. Подобные «взрывные» нагрузки категорически запрещаются людям, имеющим серьезные заболевания сердца и сосудов. Людям, у которых нет проблем с сердцем (и желающим, скажем, тренироваться в тяжелой атлетике на пределе своих возможностей), рекомендуется соблюдать особую осторожность в подходе к режиму тренировок и структуре самой тренировке. Особую опасность составляет именно повторяющиеся предельные нагрузки взрывного характера. Для больного ишемической болезнью сердца, например, даже единственная нагрузка может стать последней.

Динамические нагрузки

Динамические нагрузки – это такие, при которых напряжение мышц чередуется с их расслаблением. Примерами динамических нагрузок являются ходьба, бег, плаванье.

Работающим мышцам требуется больше кислорода, поэтому сердце усиливает свои сокращения и учащает их. Активируется гормональная система надпочечников и щитовидной железы (при ожирении, например, эта система всегда угнетена), усиливается сгорание углеводов, повышается усвоение мышцами кислорода. Активируются системы, оказывающие гипотензивное (снижающее АД) действие. Мышцы то сжимают сосуды, выталкивая из них кровь, то отпускают их, позволяя сосудам наполняться кровью. Мы получаем как бы второе, «мышечное» сердце, которое помогает нашему сердцу, разгружает его (теперь понятно, почему даже больным инфарктом миокарда и сердечной недостаточностью рекомендуются неспешные прогулки!).

Если физическая нагрузка повышается, потребности организма в энергетическом обеспечении резко повышаются. Растет потребление кислорода (так как кислород — необходимый субстрат для воспроизводства энергии). Если до этого источником энергии, в основном, было «сгорание» углеводов, то теперь в качестве источника энергии начинают выступать жиры. «Сгорание» жиров начинается примерно через 15 — 20 минут работы. Отсюда вывод: если вам необходимо сбросить вес, лишние калории или поступивший с пищей избыток холестерина, физическая нагрузка должна быть не менее 20 минут.

Во время динамических нагрузок повышается артериальное давление, частота пульса, содержание в крови адреналина и других активизирующих гормонов. Если подобная нагрузка продолжается не слишком долго, то сердце и весь организм получают хорошую тренирующую нагрузку.

А если нагрузку увеличить?

К сожалению, на определенном этапе прирост нагрузки перестает давать адекватное увеличение работоспособности сердца, наступает так называемая фаза «плато» нагрузки, «кислородный предел», за которым нагрузка начинает стремительно разрушать организм: происходит повреждение мышечной системы, сердца, сосудов, головного мозга, нарушаются газовый, белковый, углеводный, жировой, гормональный и другие виды обмена веществ и т.д. (хорошо известное заболевание спортсменов, известное как миокардиодистрофия вследствие физического напряжения).

Как дозировать нагрузку

Важно уметь хотя бы приблизительно оценивать свои физические возможности. Для определения физической работоспособности существуют различные способы. Самым простым способом дозирования нагрузок является определение максимального и субмаксимального пульса. Максимальным пульсом называется частота пульса, при которой достигается максимально возможное потребление кислорода работающими мышцами. Если нагрузка продолжает нарастать и далее, начинаются различные повреждения мышечных клеток. Существуют специальные таблицы, определяющие максимальный пульс для каждого возраста, но есть и известная упрощенная формула: 220 — возраст (т.е., если вам 45, то ваш максимально допустимый пульс равен 220 — 45 = 175).

Субмаксимальный пульс рассчитывается как 75 — 85 % от максимального. Людям, имеющим проблемы с сердцем, субмаксимальный пульс устанавливается в 75%, людям тренированным и практически здоровым можно считать субмаксимальным пульс в 85% от максимально допустимого.

Умеренные ежедневные физические тренировки (конечно, на фоне терапии) позволяют снизить уровень нейрогормонов, повысить чувствительность к медикаментозному лечению и переносимость нагрузок, а следовательно, и эмоциональный тонус, и «качество жизни». Перед началом самостоятельных занятий нужно обязательно проконсультироваться с лечащим врачом. Если вам больше 30 лет, то перед началом занятий нужно сделать электрокардиограмму. Врач должен рекомендовать вам наиболее подходящий вид физических упражнений и помочь в разработке индивидуальной программы физических тренировок. Например, людям старше 40 рекомендуется начинать с дозированной ходьбы, постепенно увеличивая темп и дистанцию. Страдающим ожирением рекомендуется более медленный темп и длительный период тренировки.

И не забывайте, что «избыточные» физические нагрузки могут привести к трагическому финалу!

Зарядка не вставая с постели

Этот комплекс выполняется сразу же после того, как вы проснулись, в постели, не более 5 минут. В результате таких занятий вы получите отличное настроение, превосходную работоспособность, а главное, здоровый дух.

Упражнение 1 — вращение ступней в разных плоскостях;

упражнение 2 — сжимание и разжимание пальцев рук;

упражнение 3 — попеременное и одновременное поднятие рук;

упражнение 4- потягивание лежа на спине и животе;

упражнение 5 — вращение головой в разных плоскостях;

упражнение 6 — наклоны туловища вперед-назад, влево-вправо, сидя на кровати.

Оценить субъективную величину нагрузки можно по степени усталости, для чего предлагаем упрощенную, но вполне действенную схему в виде таблицы.

Признак	Степень усталости
	Малая	Средняя	Большая
Цвет кожи	Покраснение	Значительное покраснение	Побагровение, синюшность губ, бледность
Потение	Небольшое	Значительное, выше пояса	Значительное, ниже пояса
Дыхание	Учащенное ритмичное	Очень быстрое, иногда ртом	Очень быстрое, неритмичное, ртом
Движения	Правильные	Небольшие нарушения	Некоординированные
Ощущения	Ничего не беспокоит	Усталость, боль в ногах, одышка, тахикардия	Усталость, головная боль, тошнота, головокружение